مساله
روش های حل مساله
1- رسم شکل
۲- تنظیم جدول نظام دار
۳- حذف حالت های نامطلوب
۴-الگو یابی
۵- حدس و آزمایش
۶- زیر مسئله ( مسئله های درون مسئله )
۷- مسئله ی ساده تر و مرتبط با مسئله ی اصلی
۸- جبر ( الگو سازی جبری )
سنسور ربات مسیریاب

مدار سنسور ساخته شده توسط دانش آموز اصلانی

مدار سنسور ساخته شده توسط دانش آموز امیر حسین راعی

مدار سنسور ساخته شده توسط دانش آموز احمدی

مدار سنسور ساخته شده توسط دانش آموز امیر رضا راعی
تربیع دایره
از امیر رضا زارعی:
تربیع دایره
ترسیم مربعی که مساحتش با مساحت دایره ای مفروض برابر باشد.
تکلیف مسئلة تربیع دایره را سرانجام فردیناند لیندمان ، ریاضیدان آلمانی ، در با اثبات غیرجبری بودن عددpروشن کرد. معنای حکم او این است که
p نمی تواند ریشة معادله ای جبری با ضریبهای صحیح باشد و بنابراین ، مسئلة هندسیِ یافتنِ مربعی هم مساحت با دایرة مفروض نه با خط کش و پرگار حل شدنی است نه با سایر منحنیهای جبری مثل مقاطع مخروطی که در تثلیث زاویه و تضعیف مکعب به کار می روند.
نظریه ی گالوا
به نام خدا
ازسیّد سینا حسینی
زندگینامه ریاضیدان مشهور اواریست گالوا

«اواریست گالوا» (Evariste Galois) در 25 اکتبر سال 1811 دربورگلاراین» (Bourg la Reine) در نزدیکی شهر پاریس فرانسه متولّد شد.
«گالوا» که برای توسعه تکنیک های جدید حل معادلاتی که امروزه به نام «نظریه گروه» معروف است، تلاش بسیار کرد.
از ریاضیدانان هم عصر با او می توان «آبل» را نام برد.
او نشان داد که معادلات کلی درجه پنجم و معادلات چند جمله ای با درجات بالاتر در تعداد متناهی و عملیات منطقی قابل حل شدن نمی باشد و ریشه آن به دست نخواهد آمد.
«گالوا» یک مقاله که شامل مهم ترین نتایج به دست آمده از تحقیقاتش بود را به «کوشی» (Cauchy) داد، بدون آن که رو نوشتی از آن برای خود نگه دارد و «کوشی» آن را گم کرد.
وقتی «گالوا» مقاله اش را برای دریافت جایزه آکادمی ریاضی ارائه کرد، «فوریه» (Furier) مقاله را برای بررسی های بیشتر به خانه برد. اما در فاصله زمانی بسیار کوتاهی درگذشت و این مقاله گم شد.
«گالوا» نسخه دوم مقاله اش را به آکادمی فرستاد.
این بار قضاوت درباره مقاله، بر عهده «پواسون» ((poisson بود.
«پواسون» دومین مقاله را که شامل نتایج مهمی درباره نظریه گروهها بود خواند.
. . . بقیه ی ماجرا را از وب خودتان ! ! !
قضیه ی گالوا:
معادلات جبری درجه بالاتر یا مساوی با 5 را نمی توان با اعمال جبری مقدماتی ( رادیکال ها ) حل کرد.
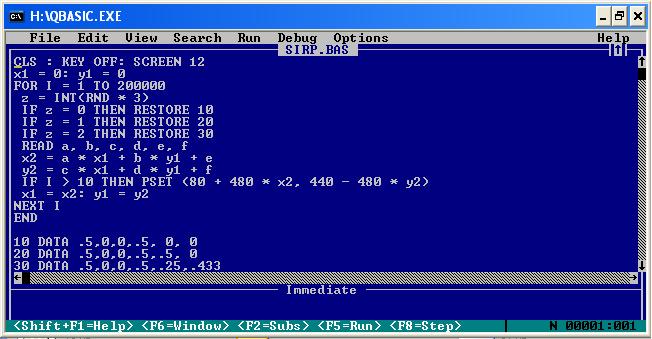
مثلث سرپینسکی
هندسه ی فراکتال
توسط مندلبرات Mandelbrot معرفی شد.
اشکال فراکتالی برای مدلسازی پدیده های طبیعی که توسط هندسه ی اقلیدسی قابل بیان نیستند، به کار می رود. مانند ابرها، شاخ و برگ درختان، کناره ی دریاها و . . .
ویژگی اشکال فراکتالی خود شبیه بودن این اشکال است.
به این صورت که هر جزء این اشکال در حقیقت مقیاس کوچکی از کل شکل است.
درختان مثال بارزی از این ویژگی هستند.
ساقه و شاخه های درخت و حتی برگ ها در واقع مقیاس کوچکی از خود درخت هستند.
در ریاضی اشکال خود شبیه فراکتالی با اعمال بینهایت بار الگوریتم خاصی بر یک شکل پایه بدست می آیند.
در عمل این کار امکان پذیر نیست و معمولا تا تکرار معینی الگوریتم را اعمال می کنند.
اشکال فراکتالی با توجه به ویژگی خود شبیه بودن، در بسیاری از موارد عملی از کاربرد دارند.
برنامه ی زیر را اجرا و از نتیجه ی آن لذت ببرید
تبدیل مثلث بزرگتر به کوچکتر - - transform - طول هر مثلث کوچکتر.نصف مثلث بزرگتر
هندسه های نا اقلیدسی - از سینا حسینی
اشکالات وارد بر هندسه اقلیدسی :
اصل اول - از هر نقطه میتوان خط مستقیمی به هر نقطه دیگری کشید یا اینکه کوتاهترین فاصله مابین دو نقطه یک پاره خط مستقیم است .
اصل دوم - هر پاره خط مستقیم را میتوان روی همان خط بهطور نامحدود امتداد داد .
اصل سوم - میتوان دایرهای به هر نقطه دلخواه به عنوان مرکز آن و با شعاعی مساوی هر پاره خط رسم کرد
اصل چهارم - همه زوایای قائمه با هم مساوی هستند .
اصل پنجم - از یک نقطه خارج یک خط ، یک و تنها یک خط میتوان موازی با خط مفروض رسم کرد .
طبق تعاریف فعلی " اصل پنجم اقلیدس که ایجاز سایر اصول را نداشت ، به هیچ وجه واجد صفت بدیهی نبود . در واقع این اصل بیشتر به یک قضیه شباهت داشت تا به یک اصل .
اشیا در دنیای فیزیکی با هندسه اقلیدسی سازگارند و هندسههای نااقلیدسی زیر مجموعهای از هندسه اقلیدسی محسوب میشوند به طور مثال یک مکعب را در نظر بگیرید که در فضای اقلیدسی ، از نظر هندسی کاملا اقلیدسی است و اگر کره محیط یا محاط آن را رسم کنیم داخل سطح کره با هندسه هذلولی و خارج سطح کره با هندسه بیضوی برسی و مطالعه میشود.
در هندسه اقلیدسی هر پاره خط مستقیمی میتواند بیانگر یک عدد باشد که بیانگر طول واقعی آن بوده و مربع و مکعب آن مقدار درستی در محاسبات ریاضی است ولی در هندسههای نااقلیدسی چنین نیست برای اینکه طول واقعی یک منحنی میتواند یک عدد باشد ولی این منحنی نمیتواند حتما و لزوما بیانگر همان عدد باشد ، برای اینکه انحنا یافته است و طول منحنی بیشتر از فاصله دو سر منحنی میباشد و این دو مقدار با هم نامساوی هستند . به طور مثال در هندسه اقلیدسی یک مربع به ضلع 1 متر بیانگر یک متر مربع است و یک مکعب به ضلع 1 متر بیانگر یک متر مکعب است ولی در هندسههای نااقلیدسی این مقدارها متفاوت است که نیاز به در نظر گرفتن ضریبی مبنی بر درصد خطا در محاسبات داریم . اصولا انحنا در هندسههای نااقلیدسی ، به طور کلی نسبت به یک خط راست اقلیدسی مشخص و نسبت به یک دایره با شعاع واحد واقع بر یک صفحه مسطح اقلیدسی سنجیده میشود و صحت هندسههای نااقلیدسی در گرو صحت هندسه اقلیدسی است .
ریاضیات دیداری
الف) دلگون(Cardioid) :
اگر دایره ای به شعاع 1 واحد مماس بر دایره ای به شعاع 1 واحد، حول آن بغلتد،شکلی که یک نقطه از محیط دایره ی غلتان بر آن حرکت می کند را دلگون گویند .

نفروئید(Nephroid):
اگر دایره ای به شعاع 1 واحد مماس بر دایره ای به شعاع2 واحد، حول آن بغلتد،شکلی که یک نقطه از محیط دایره ی غلتان بر آن حرکت می کند را نفروئید گویند

ج)دلتاگون(Deltoid):
اگر دایره ای به شعاع 1 واحد مماس بر دایره ای به شعاع3 واحد، درون آن بغلتد،شکلی که یک نقطه از محیط دایره ی غلتان بر آن حرکت می کند را دلتاگون گویند

د)ستاره گون(Astroid):
اگر دایره ای به شعاع 1 واحد مماس بر دایره ای به شعاع4 واحد، درون آن بغلتد،شکلی که یک نقطه از محیط دایره ی غلتان بر آن حرکت می کند را ستاره گون گویند .